Logarithms(logs)/Chapter 13
Make a table like that below. Guess what the log 1 is first, (read as the log of 1, base 10), and put your guess in the table in the right-hand column, even though you probably don't know what a log is! Then use a calculator to get the log 1, to 3 decimal places- put that in the center column, under 'calculator answer'. Then guess what the log 2 is. Put that number in the right-hand guess column. Use the calculator to get the log 2 to 3 decimal places- put that under 'calculator answer'. Fill in the rest of the table this way, and look for patterns as you go.

Remember, Kavi didn't know anything about logs. When he got to log 4 = .602 Don asked if he saw anything. How did this relate to log 2 = .301? He wrote log 4= 2* log 2= log 2² . Do you see another one like this?

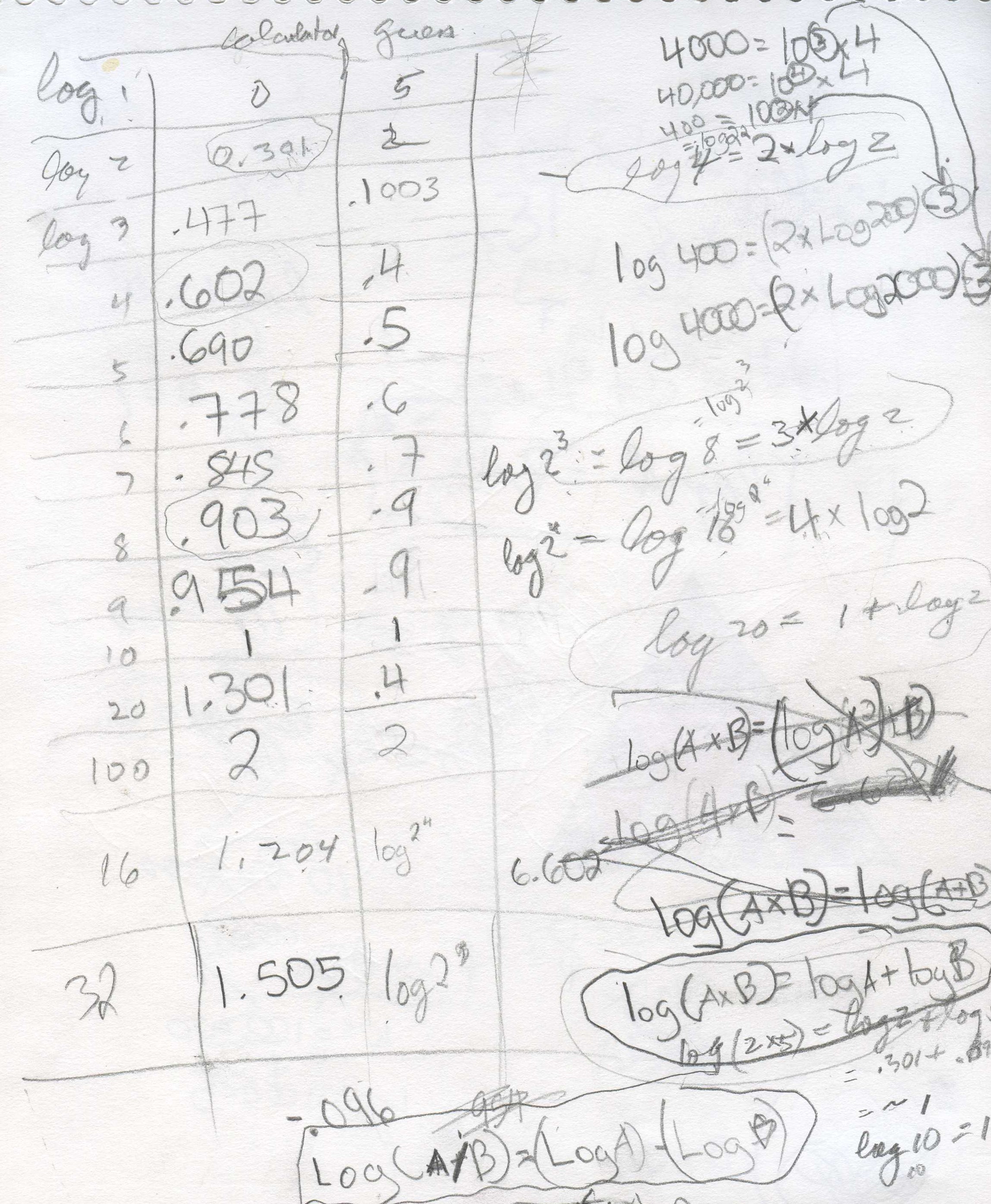
Looking for patterns, Kavi found three identities above and below:

                                       Identity #  1.)   log (A*B)= log A  +  Log B

                                       Identity #  2.)   log (A/B)= log A  -  Log B,  and

                                       Identity #  3.)   log A^B  = B*log A   and

                                             Identity #   4.)   log_A A = 1

 These idendities work for any base.   

Don also talked with Kavi about the

                                        exponential equation:  10² = 100 and the

                              corresponding log equation:  log₁₀ 100 = 2

The exponent 2 is the log; generalizing  log_B x = y  Read: the log of x, base B = y and  B^y = x

Notice: log₁₀ 10 = 1  because 10¹ = 10 and log_e e = 1 (e is the

 base of the natural logarithms) and log_A A = 1.

And log₁₀ 1 = 0  because 10⁰ = 1, and log_e 1 = 0  and log_A 1 = 0

He also found he could solve the equation: log₄ x = 3, then  x = 4³ = 64.

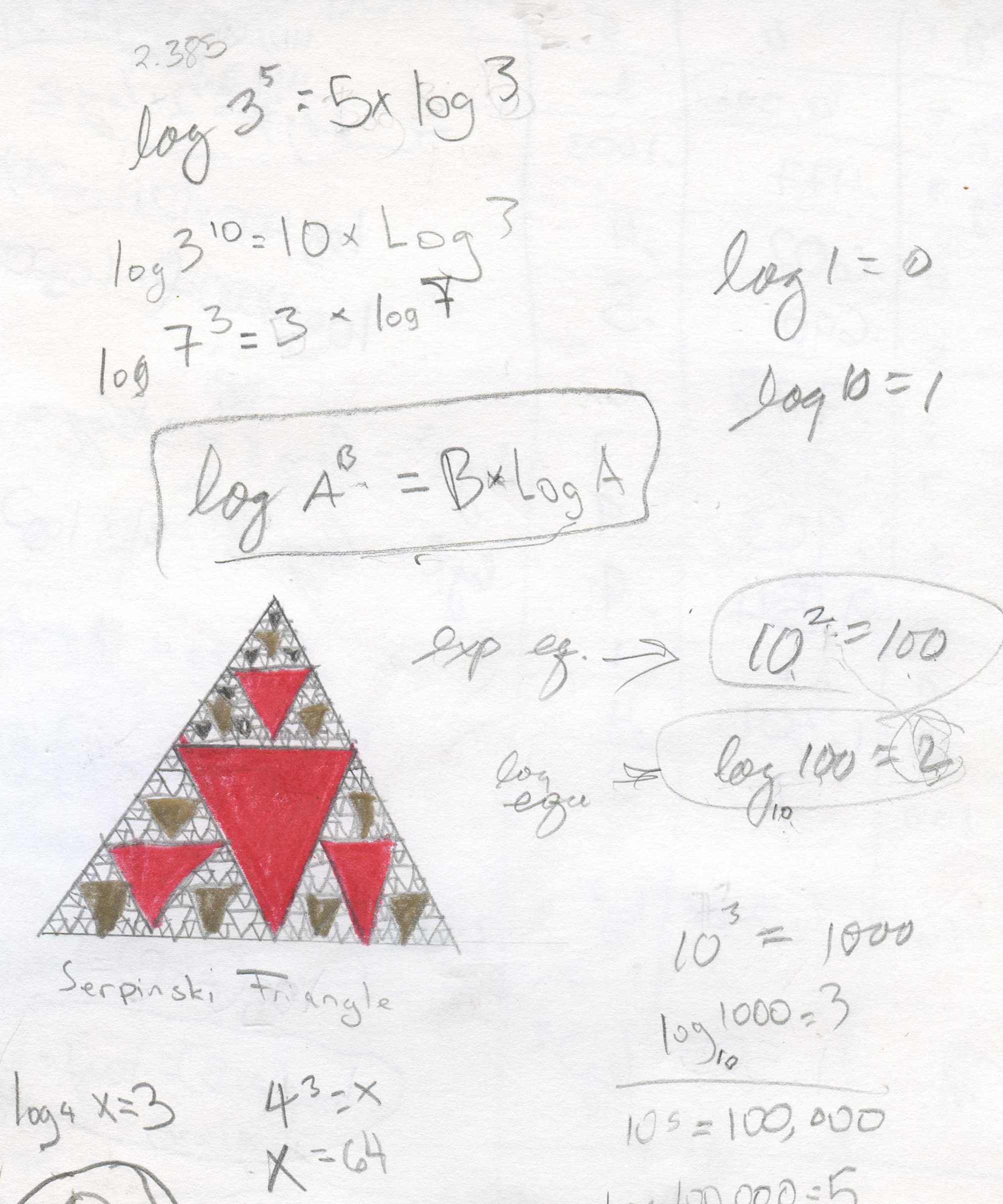
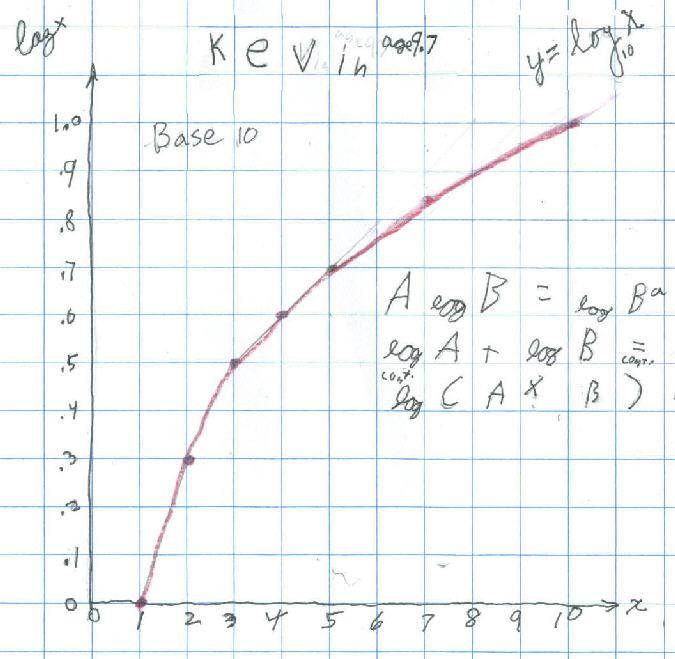
What happens to the graph when x = 1/2 ?

What about the log₇ 8 = x ? Your calculator only has base 10 or base e logs, not base 7!

Write log₇ 8 = x as an exponential equation  7^x = 8,  then take

 the log of both sides, to base 10, (or base e) to get        

                                                        log₁₀ 7^x = log₁₀ 8   using the identity # 3.,

log₁₀ A^B  = B*log₁₀ A , we get           x*log₁₀ 7 = log₁₀ 8   Now we

 can solve for x by dividing both sides by log₁₀ 7, to get        

                                                       x = log₁₀ (8)/log₁₀(7)  or

                                                        x = ln (8)/ln (7)

Either calculation, you get the same answer and we can find the log of a number in any base!

Don told Kevin about how the logarithm was invented by Napier (along with some others), and the result was to vastly increase the computational powers of astronomers like Tycho Brahe and Kepler. That was because products are changed into sums using Kevin's identity   log₁₀A +   log₁₀ B = log₁₀(AxB) and when one is dealing with large numbers, as with distances to the moon and sun, it it much simpler to add the logs, than multiply the numbers. [Also the log₁₀ 1000000 = 6.]

When students get to this point Don will usually asks them, what is the ln(^-1)? Try it on your calculator. 

                                     ln(^-1) = pi*i    which is an imaginary number. When we write this as an exponential equation, we get    E^Pi*i          = ^-1  ,  add 1 to both sides                           

  E^pi*i +  1 = 0

We end up with a true statement with the 5 most important numbers in mathematics: E, pi, i, 1  and  0. WOW!! 

See how the area under these 2 curves y=1/x and y = 1/(1+x) lead to logs