Natalie returns at age 8, to work with Don

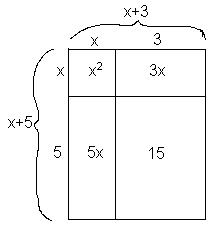
Don used the area a rectangle model to find 3*(2+5) = 3*2 + 3*5 = 6+15=21. This is the distributive property 3*(2+5) = 3*2 + 3*5 or a (b + c) = ab + ac. Then to multiply (x + 3)*(x+5) Don again drew a rectangle:

Natalie found the area to be  x² + 3x + 5x + 3x5 = x² + 8x + 15, so

 (x + 3)_*(x+5)  =  x² + 8x + 15

Don asked Natalie to look where the 8x and 15 come from. And she did  these: 4(y-3)= 4y-12

            (x+3)(x+4)= x² + 7x + 12

            (4x + 3)² = (she first wanted to say 16x² + 9), but she drew the rectangle or square, in this case, and got  16x²
+ 24x + 9. She also found
                                                (a + b)² = a² + 2ab + b²

At this point Don showed Natalie that multiplying is the opposite of factoring. This is multiplying (x+3)(x+4) to get  x² + 7x + 12. And if you factor  x² + 7x + 12, you get  (x+3)(x+4). She did both multiplying and factoring, like

             multiply (x-3)(x+7) =               

                                             = x² + 5x + 6  factor

            multiply (2x-5)(3x-7)=

                                              = 6x² - 11x - 35  factor

Natalie also used the rectangle to multiply (x+2)(3x² + 5x - 1). She ended with (x+2)(3x² + 5x - 1) = 3x³ + 11x² + 9x -2.

8/30/01 Natalie found a pyramid made from cubes and Don asked if she would find the number of cubes in each layer: 1, 3, 6, 10, 15 . Don asked if she could find the number of cubes in the 100th layer. Natalie thought about this, saw a pattern in the table below, 2+1=3, 3+3=6,... (her triangle theory). Then she said she knew the sum of the numbers from 1-9 = 45, then she wrote her theory to get the sum of the numbers from 1 to 100:

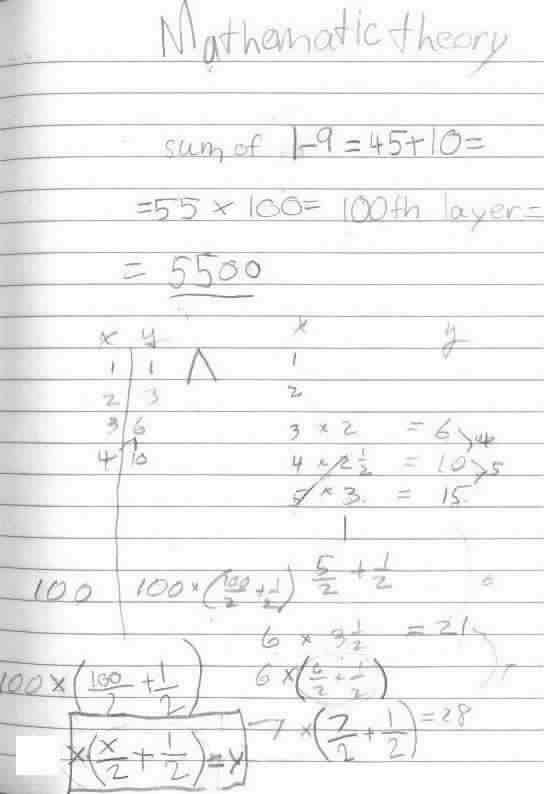
Don wrote down what she talked about above, until she saw the pattern and wrote the rule,  x(x/2 + 1/2) = y. She realized then, that her prediction of  5500 was wrong and should be 5050 for the sum of the first100 numbers.

Natalie wrote "I graphed the rule x(x/2 + 1/2) = y ." She plotted the points (1,1), (2,3), (3, 6), (4, 10) and (5, 15). Then Don asked Natalie to put in 0, -1, and -2 in for x to get the y-values and plot more points. There was a lot of arithmetic and negative number work to do here!

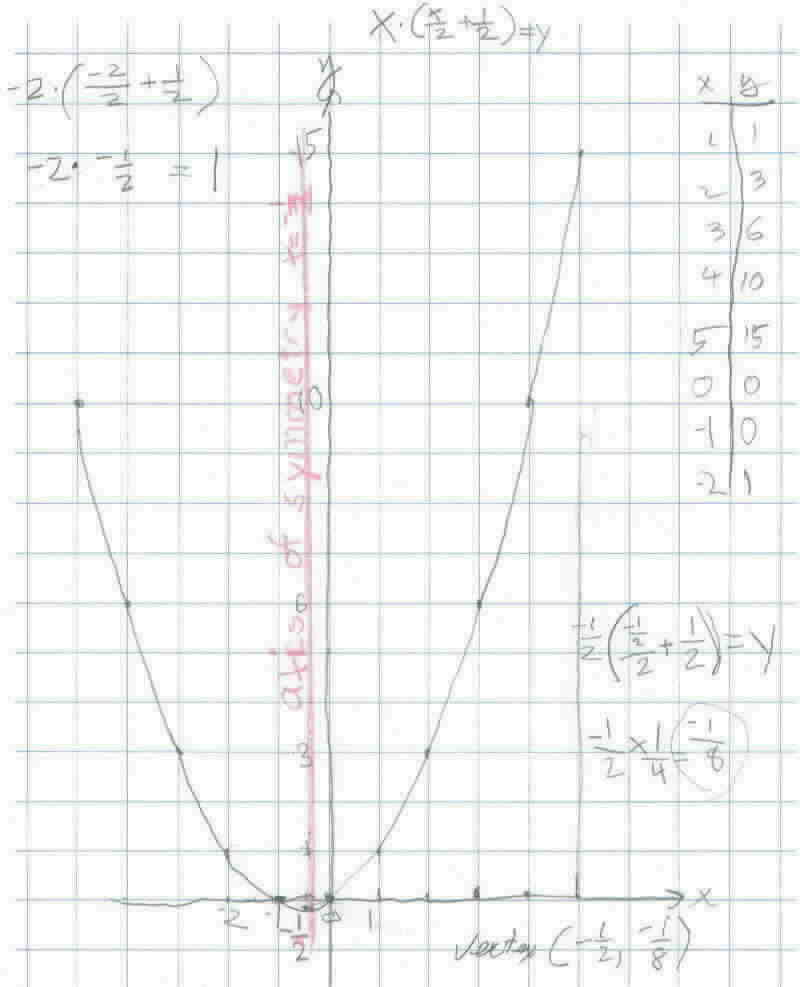
She found (0, 0), (^-1, 0) and (^-2, 1) were other points on the graph. Don asked Natalie where the axis of symmetry was. She pointed to the point ( ^-1/2, 0) and Don told her the mirror would go along the line which she drew in red, and Don told her the equation of that line was x = ^-1/2. Then Don asked her where the lowest point (the vertex) was. The x-coordinate was ^-1/2, so Don suggested she put that in for x and find y in the rule. See her work on the right bottom on the graph paper. The vertex (low point in this case) of the parabola is ( ^-1/2, ^-1/8).

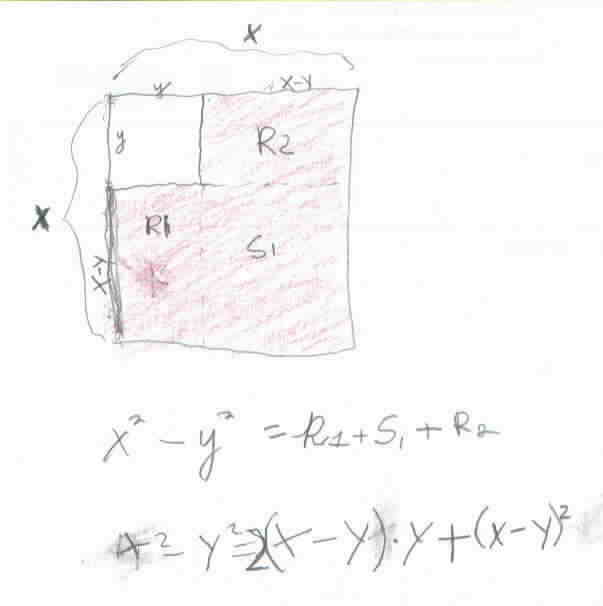
Don asked Natalie to find another name for x² - y²

8/31/01 Natalie had worked on the tower puzzle during the school year and now was ready to do the math from it. She started with 1 disk, then 2 disks, and found the minimum number of moves to move the pile. After some discussion on another piece of paper,  Natalie saw that the 7 = 2³ - 1 and 15 = 2⁴ - 1, so the rule was 2^x - 1= y. Don made sure she could work with negative exponents. The pattern tells the story:
2⁴ = 16
2³ = 8
2² = 4
2¹ = 2
What's happening to the answer as the exponent goes down 1? Natalie said "You divide by 2". So
2⁰ = 1
2^-1 = 1/2 and
2^-2 = 1/4 = 1/2² and
2^-3 = 1/8 = 1/2³

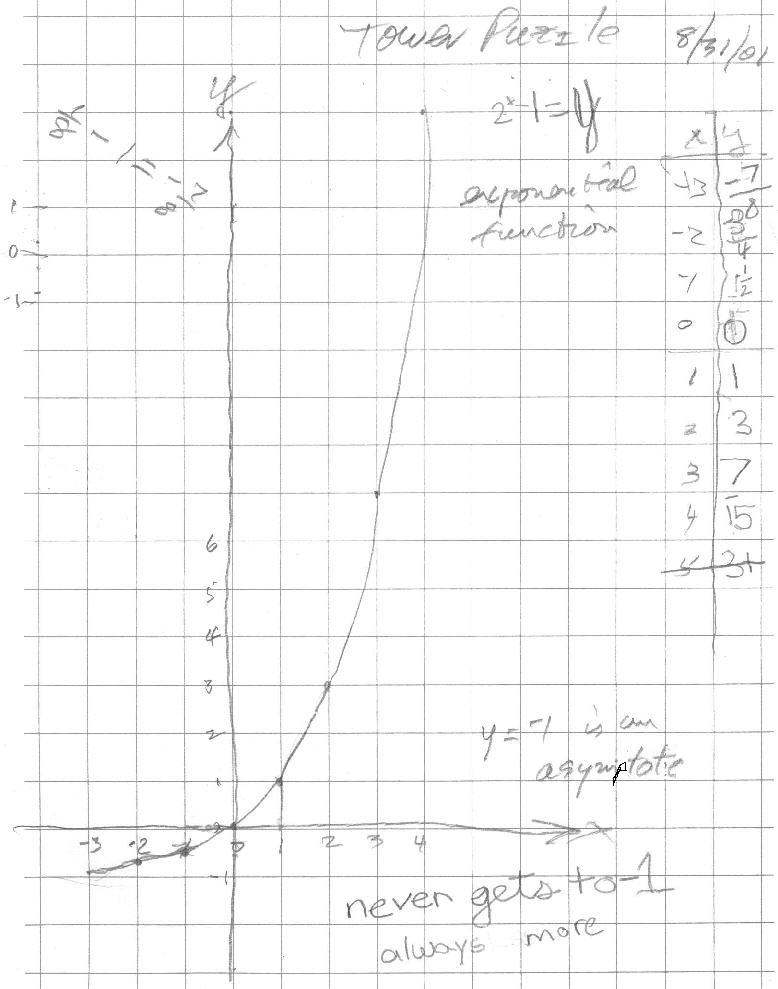
After Natalie had graphed from x = 0 to 4, she thought the graph would be a parabola. Then she put negative numbers in for x, and again did a lot of arithmetic of signed numbers and negative exponents. She realized the curve "never gets to  ^-1 always more". Don gave her the word asymptote (misspelled on the graph, and corrected),  as the line it approaches, but never reaches.

Fine job Natalie!