For the Nautilus shell,
 the ratio of
radius vectors
every 360 degrees is a constant, about 3.2. My students average their
mesurements and get pretty close to that (within 10%). The angle
comes out another constant, about 79.5 degrees; this spiral is called an
equiangular spiral because of this. A number of young people have worked
on these problems of the Nautilus shell. Vickie, a 9th grader at the
time, used the half-shell, and studied the volume increase from section
to section. I have a full and half shell in my
"Math Room". The shell is beautiful and mathematical, that's why it is my
logo. The shell on my main web site page is a copy of a watercolor
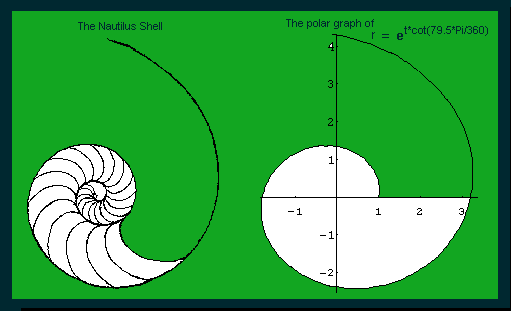
painting I did of the shell. The rubbing is on the left. The polar equation of the shell spiral is r =
et * cot (79.5*Pi/180) The polar plot of this
equation in Mathematica looks like that at right above. You can see when t
=0, r =1. A 360 degree
turn (t=2*Pi) gives an r of about 3.2, and the Nautilus grows at this constant
ratio throughout (as mentioned above). (See also Frank
Land's book "The Language of Mathematics", Doubleday, 1963).
the ratio of
radius vectors
every 360 degrees is a constant, about 3.2. My students average their
mesurements and get pretty close to that (within 10%). The angle
comes out another constant, about 79.5 degrees; this spiral is called an
equiangular spiral because of this. A number of young people have worked
on these problems of the Nautilus shell. Vickie, a 9th grader at the
time, used the half-shell, and studied the volume increase from section
to section. I have a full and half shell in my
"Math Room". The shell is beautiful and mathematical, that's why it is my
logo. The shell on my main web site page is a copy of a watercolor
painting I did of the shell. The rubbing is on the left. The polar equation of the shell spiral is r =
et * cot (79.5*Pi/180) The polar plot of this
equation in Mathematica looks like that at right above. You can see when t
=0, r =1. A 360 degree
turn (t=2*Pi) gives an r of about 3.2, and the Nautilus grows at this constant
ratio throughout (as mentioned above). (See also Frank
Land's book "The Language of Mathematics", Doubleday, 1963).

