Eva shares 5 cookie between 3 people!
Eva shared 1 cookie with each person, with 2 cookies left over.
Then she cut one of the leftover cookies into 4 pieces, each piece 1/4. She
shared 1/4 with each person, leaving 1 cookie and 1/4, and each person has 1 +
1/4 cookies so far.
Eva then cut the whole cookie and the 1/4 into eighths. She had 8/8 + 2/8 =
10/8. She shared 3/8 of a cookie with each person, with 1/8 left over. Each
person then had 1 + 1/4 + 3/8 cookies. Eva then continued to cut each leftover
piece into 4 pieces, sharing 1 with each person, with 1 left over! 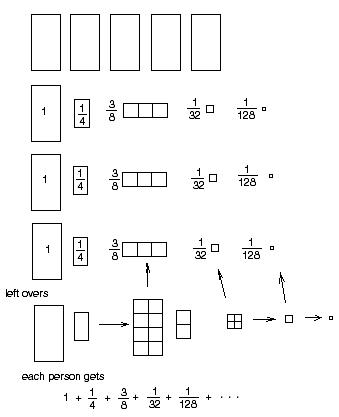
Her method resulted in an infinite series!
Eva went on to do the same problem a different way, and each person got 1 + 2/3
cookies.
So 1 2/3 = 1 + 1/4 + 3/8 + 1/32 + 1/128 + ...
This got us into a discussion of fractions and decimal equivalents and adding
the infinite series to see what it gets close to. All very interesting!
Betty, a fifth grade teacher (her son is working on the SAT test with Don
also), got 5/3 for Eva's problem. I asked Betty to read Eva's solution to the
problem and she realized that 1 2/3 = 1.666... an infinite repeating decimal,
which is also an infinite series 1 + 6/10 + 6/100 + 6/1000 + ... Betty raised
the question: If you can add 6/10 + 6/100 + 6/1000 + ... could you also multiply
6/10 x 6/100 x 6/1000 x ... ? A wonderful question! Betty proceeded to use a
calculator to multiply 6/10 x 6/100 x 6/1000 and ended up with the number
2.16E-4. We had a big discussion about what this meant. 2.16E-4 means 2.16*10-4,
or .000216 . Let's see what happens now!
To other discoveries
To download
Don's materials
Mathman home
