Geometric Sequences and

The Frequencies of the 88 Keys on a Piano

(The Equal Tempered Chromatic Musical Scale)

By Don Cohen- The Mathman

February, 2006

A geometric sequence is found by starting with a number, then multiplying this by a 'certain number'. Whatever one gets, you multiply that answer by that same 'certain number', and continue that.  The multiplying number is always the ratio of two consecutive numbers in the sequence. For example, let's start with 3, and let our multiplying number (that 'certain number' )or ratio, be 2, and write the first 4 terms of this geometric sequence.

3,  3*2,  3*2*2,  3*2*2*2,.. , or using exponents: 3*2⁰ , 3*2¹ , 3*2² , 3*2³ or  3, 6,12, 24, ..    (Notice 2⁰  =1, 2¹  =2,  2²  =4,  2³  =8).. What's the ratio of consecutive numbers in the sequence? Well 6/3 = 2,  12/6 = 2,  and 24/12 = 2 ..

Problem 1: If the first number of a geometric sequence is 1 and the fourth number in the geometric sequence is 64, what are the second and third number in the geometric sequence, or what are the two geometric means between 1 and 64?  1,  ?   , ?  , 64

Solution 1: 1= 1*r⁰, (r being the ratio), the second number is 1*r¹, the third term is 1*r² and the fourth number is 1*r³ = 64, so r³ = 64. What number cubed, or multiplied by itself 3 times = 64 or

^{what is the cube root of 64 or ?  4. Because 4*4*4 = 64, so r = 4. Our geometric sequence then is 1, 4, 16,  64.}

Problem 2: If the first number of a geometric sequence is 1 and the thirteenth number in the geometric sequence is 2, what are the 2nd through 12^th numbers in the geometric sequence, or the 11 geometric means between 1 and 2?

Solution 2:  1       2       3       4        5       6       7        8      9      10      11        12         13

                  1= r⁰ , 1*r¹ , 1*r² , 1*r³ , 1*r⁴ , 1*r⁵ , 1*r⁶ , 1*r⁷ , 1*r⁸,  1*r⁹ , 1*r¹⁰  ,  1*r¹¹  ,  1*r¹²

                      1 ,   ?   ,    ?    ,  ?    ,  ?    ,  ?    ,   ? ,     ?   ,   ?  ,    ?   ,    ?  ,        ?   ,       2                                                                                                       

^{So  r12  =   2   and  r = = 1.05946'}

The subscript ₃ below indicates the 3^rd octave, if one starts with the 0^th octave A₀ = 27.5 Hertz (vibrations/sec),

If the first term, instead of 1, is middle C₃ = 261.63 Hz, in the equal tempered chromatic scale,

                           the second term is  C₃^# = 261.63*1.0594 = 261.63* = 277.18 Hz and

                                                            D₃ = 261.63*1.0594² = 261.63* = 293.66 Hz and

                                                            D₃^# = 261.63*1.0594³ = 261.63* = 311.12 Hz..

                                                       to  A₄  = 261.63*1.0594⁹ = 261.63* = 440.00 Hz .. 

                                                 to  C₄   = 261.63*1.0594¹² = 261.63* = C ₃*2 = 523.25 Hz.   C₄ is double the frequency of C ₃ , and an octave higher than C _{3 .}

An octave is divided into twelve intervals to form the equal tempered chromatic scale; the Intervals ^{of pitch are described in terms of the ratios of the frequencies ~1.0594 =}                                                    

The frequency of each note in the scale can be figured by multiplying each successive note by this number to get the next. The frequency of any note can also be figured from A₀ = 27.5 Hz, using the formula:

f(N) = 27.5*2^(N/12),  where N is an index into the equal tempered chromatic scale notes starting with N= 0 for A₀, the lowest note on the keyboard. N increases by 1 for each note on the keyboard. Note that the actual key on the keyboard is N + 1. The 88^th key has a frequency for N=87 in the formula above, so f(87) = 27.5*2^(87/12) = 4186.009 Hz, the frequency of the note C₇

The table below shows the note, the index number (N) and corresponding frequencies (f) and the Octave for all of the keyboard notes based on A₄ = 440 Hz  in the equal tempered chromatic scale.

The modern piano has 88 keys (seven octaves = 7*12 = 84, then add 4 to get 88. The 4 is a minor third = (1/3)*12= 4; so the 88 piano key notes go from from A₀, the lowest note, or 27.5 Hz, to C_7,  the highest note on the piano, 4186.009 Hz.  

The following graph done in Mathematica, shows a polar graph of the frequencies for the octave from middle C ₃ (261.63) to C₄ (523.25). Each point has as its distance from the origin (or radius) the pitch or frequency, and the angle from the starting position is (360/13)*n, starting with n=0, going counterclockwise. The command to do this graph is:  PolarListPlot[Table[261.6256*2^(n/12),{n,0,12}],PlotStyle->PointSize[0.02]].

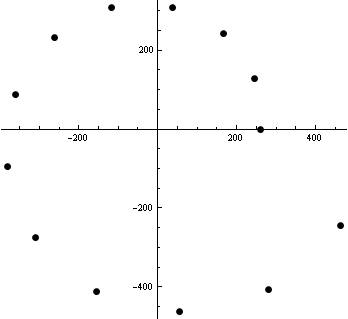
In trying to understand how all this works, Don found these two sources very helpful:

'The Handbook of Chemistry and Physics' (26^th edition) edited by Charles D. Hodgman and Harry N. Holmes, Published in 1942 by Chemical Rubber Publishing Co., Cleveland, OH

An internet file 'The Equal Tempered Scale and Some Peculiarities of Piano Tuning' with the table above, by Jim Campbell