)^n)*'^('*n*p/4)],Some
uses of MATHEMATICA in Don's
teaching
The latest one: Rotating a sine wave 60 degrees ccw.
1. Go to A Map to Calculus , click on 'Iteration or Feedback' (upper left), and see the patterns Maura finds.
2. Go to A Map to Calculus , at lower right , click on 'Find the Sqrt 40 by averaging and iterating'
3. Don and three of his students found the Dottie
number, at http://www.mathman.biz/html/Dottie_Number.html
).
4. Have
Mathematica graph 2 iterations of y=5-6/x (an infinite continued
fraction, from solving the quadratic equation x2-5x+6=0,
whose roots are {2,3}). Where do the curves intersect and what kind of curve is
each one?
5. Anae plotted (2+i)n for n = whole numbers, without Mathematica, then Don plotted (1+i)n where n is a whole number, using Mathematica to get a spiral. He then wrote the coordinates in complex number form, eix form and cis form. Click on '(1+i)n spiral' on Don's A Map to Calculus (at the bottom) . Three spirals were then plotted using Mathematica, with the following commands:
ParametricPlot[{Re[(1+
')^n],Im[(1+
')^n]},{n,0,12}]
)^n)*'^('*n*p/4)],
Im[((
)^n)*'^(
' *n*p/4)]},{n,0,12}]
ParametricPlot[{Re[(()^n)*(Cos[n* p /4]+ '*Sin[n* p /4])],
Im[(()^n)*(Cos[n* p /4]+ '*Sin[n* p /4])]},{n,0,12}]
6. Graph
of iterations of i^i -> fractals! (notice
that i^i is a real number!)
See IES applet based on Don's i^i , in chapter 11, linked
on that page and they get fractals!
7. Using Mathematica as one of 3 ways to find, and click on 'the vol of a pyramid/Vol of a cube (with the same base)' on Don's A Map to Calculus
8. Using Mathematica to make a list of the first 30 Fibonacci numbers.
10. Don uses Mathematica to make a polar graph of r = 2t , a spiral, then sees if 90' segments are similar shapes using 'the eye test'. Click on 'spirals r = 2t ' on Don's A Map to Calculus (left and below Graphs)
11.
Don uses Mathematica to make a polar
graph of the Nautilus Shell equation and compares it to a rubbing of the shell
and the measurements his students make of the shell.
12. Ian uses Mathematica to graph the output of his rule which finds E using polypowers. Click on 'Infinite Sequences' on Don's A Map to Calculus
13. Find, and graph, the three cube roots of 8. A good lead into de Moivre's theorem.
14. Click on 'derivatives'
on Don's A
Map to Calculus , go to '
15. David's
method gets a polynomial function for Don's pairs of numbers, made
much simpler with Mathematica.
16. Geoffrey uses Mathematica in his study of polypowers
17. Use of Mathematica in Ch.11 answers
18. His Dad worked with Geoffrey using Mathematica to do the infinite sum
19. Fractions to decimals by MaggieP
20. SeeLori Johnson Morse's 4 Wolfram Demonstration Projects, based on Don's book Changing Shapes With Matrices
21. Don graphed 1/x in Mathematica and found the following: The area under the curve 1/x from 1 to 3 is equal to the loge 3 = ~ 1.0986 ...
22. Don showed Michael how to do this in Mathematica' and Derive. Michael tried things to show how his rule works for big numbers. ...
23. .The graph of (1 + 1/n)^n by Geoffrey in Mathematica' approaches E
24. Infinite Continued Fractions method #4
25.
(I graphed the
ellipse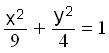 
in Mathematica,
rotated it 90o
CCW, then I copied them into my paint program where I..
26. The following graph (bottom of page) done in Mathematica, shows a polar graph of the frequencies for the octave from middle C 3 (261.63) to C4 (523.25).
27. , June 16, 2008 ... Don showed Nanako and Mum how Mathematica can get 100 digits for The Golden Mean quickly: N[(Sqrt[5]+1)/2100] = ... (at the bottom of the page).
29. Geoffrey, a 6th grader, works on polypowers
30.Tim finds a new way to write the nth term of an infinite geometric series
31. Moving a graph, write the equation.
33.
